
This can be avoided if, on the ith step (when x 1.
This brute-force method will require occasional retries whenever the random number picked is a repeat of a number already selected. One method of generating a random permutation of a set of size n uniformly at random (i.e., each of the n! permutations is equally likely to appear) is to generate a sequence by taking a random number between 1 and n sequentially, ensuring that there is no repetition, and interpreting this sequence ( x 1. Generating random permutations Entry-by-entry brute force method A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation. Your results will be pretty unpredictable nonsense unless the problem is constrained enough that models can find a somewhat stable function (or decision surface or whatever).Sequence where any order is equally likelyĪ random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. You want $N$, the number of samples, to be much much greater than $p$, because curse of dimensionality: You can't really fill the super-high-dimensional 1000-dimensional space with examples its volume is just too large. If you're concerned about duplication of information across features, and because you have an absurd number of features, consider feature reduction techniques. As you mention, each node already takes a random subset of features to decide splits, so in a way you already get your scramble. Sklearn's random forest has _feature_importances, for example. Generally you can just train a random forest on your data and then look to see how many nodes chose particular features as the one to split on. Maybe you could devise some crazy Hamming distance scheme to figure out how much to weight the inaccuracies of models training on scrambled datasets, but this seems like it would require a lot of models and be computationally expensive, and it shouldn't be necessary. I wouldn't take either of these approaches to decide feature importance, because when I misplace a column, I don't just misplace it in isolation I displace the one where it has to go.
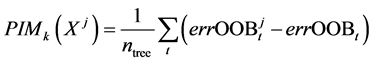
Or if you train on the canonical order, then the scrambled order looks scrambled. To answer your question, it seems the same to me whether you scramble columns in the set you train on or before you pass the test set: Effectively if you scramble before training, the model expects things in scrambled order, and then the canonical order looks scrambled to it. My question is: Is this approach valid? Is permutation of variables in the training set a better approach in general? If not, in which cases would it be not appropriate? Therefore, I'm thinking about changing my approach in the sense that I'm permuting the variables in the training set and not in the test set.

If I now permute the corresponding columns of the test set, it is clear that the performance will drop, although this does not indicate whether these variables hold unique information at all. The variables are predictive and and due to sub-sampling of variables at each split, they will get selected during model training. However, in the above case, the assumption does not hold. In these cases my assumption under H0 is that these variables are completely uninformative and thus it shouldn't matter whether I permute the column of the training or test set.

I first bootstrap from the training data and build a random forest model and then permute the columns in the out-of-bootstrap samples and check if I observe a significant decline in accuracy. My general approach for testing the significance of the importance of variables is a bootstrap permutation test, i.e. However, these variables are highly correlated and thus it is unclear whether each variable actually holds unique information or simply ranks high due to correlation to the causal variable. I have a rather high-dimensional data set ( p > 1000) with several variables ranking significantly higher than the rest in terms of variable importance (measured by Gini impurity).


 0 kommentar(er)
0 kommentar(er)
